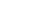Simplify Square Root of 12012

Here we will show you two methods that you can use to simplify the square root of 12012. In other words, we will show you how to find the square root of 12012 in its simplest radical form using two different methods.

To be more specific, we have created an illustration below showing what we want to calculate. Our goal is to make "A" outside the radical (√) as large as possible, and "B" inside the radical (√) as small as possible.

√12012 = A√B

Greatest Perfect Square Factor Method
The Greatest Perfect Square Factor Method uses the greatest perfect square factor of 12012 to simplify the square root of 12012. This is how to calculate A and B using this method:

A = Calculate the square root of the greatest perfect square from the list of all factors of 12012. The factors of 12012 are 1, 2, 3, 4, 6, 7, 11, 12, 13, 14, 21, 22, 26, 28, 33, 39, 42, 44, 52, 66, 77, 78, 84, 91, 132, 143, 154, 156, 182, 231, 273, 286, 308, 364, 429, 462, 546, 572, 858, 924, 1001, 1092, 1716, 2002, 3003, 4004, 6006, and 12012. Furthermore, the greatest perfect square on this list is 4 and the square root of 4 is 2. Therefore, A equals 2.

B = Calculate 12012 divided by the greatest perfect square from the list of all factors of 12012. We determined above that the greatest perfect square from the list of all factors of 12012 is 4. Furthermore, 12012 divided by 4 is 3003, therefore B equals 3003.

Now we have A and B and can get our answer to 12012 in its simplest radical form as follows:

√12012 = A√B

√12012 = 2√3003

Double Prime Factor Method
The Double Prime Factor Method uses the prime factors of 12012 to simplify the square root of 12012 to its simplest form possible. This is how to calculate A and B using this method:

A = Multiply all the double prime factors (pairs) of 12012 and then take the square root of that product. The prime factors that multiply together to make 12012 are 2 x 2 x 3 x 7 x 11 x 13. When we strip out the pairs only, we get 2 x 2 = 4 and the square root of 4 is 2. Therefore, A equals 2.

B = Divide 12012 by the number (A) squared. 2 squared is 4 and 12012 divided by 4 is 3003. Therefore, B equals 3003.

Once again we have A and B and can get our answer to 12012 in its simplest radical form as follows:

√12012 = A√B

√12012 = 2√3003

Simplify Square Root
Please enter another square root in the box below for us to simplify.

Simplify Square Root of 12013
Here is the next square root on our list that we have simplifed for you.